| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- postorder
- 데이터전문기관
- classification
- broscoding
- KNeighborsClassifier
- 웹 용어
- paragraph
- inorder
- bccard
- html
- tensorflow
- pycharm
- web 개발
- web
- 자료구조
- 결합전문기관
- vscode
- 대이터
- discrete_scatter
- 머신러닝
- web 용어
- Keras
- java역사
- C언어
- web 사진
- 재귀함수
- cudnn
- mglearn
- CES 2O21 참가
- CES 2O21 참여
- Today
- Total
목록분류 전체보기 (688)
bro's coding
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import load_iris iris=load_iris() iris dir(iris) ['DESCR', 'data', 'feature_names', 'target', 'target_names'] iris.data.shape (150, 4) iris.feature_names ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)'] iris.target_names array(['setosa', 'versicolor', 'virginica'], dtype='
 sklearn.오류값 찾기
sklearn.오류값 찾기
https://broscoding.tistory.com/112 머신러닝.수치근사법 import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs data,label=make_blobs(n_samples=500,centers=[[0,0]]) data plt.hlines([0],-10,10,linestyles=':') plt.vlines(.. broscoding.tistory.com X=np.random.randn(500)*5 # 곱하는 수의 절댓값이 커질수록 직선에 가까워진다. y=X+np.random.randn(500) # 곱하는 수에 따라 회전(기울기 개념) pred_y=2*X # 기울기를 변경해 가며 ..
 sklearn.수치근사법
sklearn.수치근사법
import numpy as np import matplotlib.pyplot as plt from sklearn.datasets import make_blobs data,label=make_blobs(n_samples=500,centers=[[0,0]]) data plt.hlines([0],-10,10,linestyles=':') plt.vlines([0],-10,10,linestyles=':') plt.scatter(data[:,0],data[:,1],alpha=0.3) plt.axis('scaled') data=data*[3,1] plt.hlines([0],-10,10,linestyles=':') plt.vlines([0],-10,10,linestyles=':') plt.scatter(data[:,..
#기울기 : coef(각각의 차원에 대한 기울기) #y절편 : intercept_ # ex: #coef의 결과 : a, b, c #intercept_의 결과 : d # data:XYZ # aX+bY+cZ=d # 각 데이터의 기울기( 가중치 ) : a, b, c # target의 높이 : d -기울기 : coef(각각의 차원에 대한 기울기) -y절편 : intercept_ ex: coef의 결과 : a, b, c intercept_의 결과 : d data:XYZ aX+bY+cZ=d # 각 데이터의 기울기( 가중치 ) : a, b, c # target의 높이 : d model.coef_ array([-0.21027133, 0.22877721, 0.52608818]) a=-0.21027133, b=0.2287..
- 비용함수는 예측한 값과 실제 값과의 차이를 수치화하는 방법(함수)이다. - 위의 결과에서 예측값인 평균값과 실제 데이터의 값들과의 차이로 계산
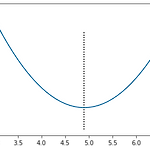 sklearn.비용함수.경사 하강법(stochastic gradient descent)
sklearn.비용함수.경사 하강법(stochastic gradient descent)
stochastic gradient descent rng=np.arange(mm-2,mm+2,0.1) plt.plot(rng,((data-rng.reshape(-1,1))**2).mean(axis=1)) plt.vlines([mm],11,15,linestyles=':') plt.ylabel=('MSE') plt.xlabel=('prediction') # 평균일 때, 오차가 가장 작고 # 평균과 멀어지면 오차는 증가한다.
#MAE(절댓값 에러) (np.abs(data-data.mean())).mean() #MSE(제곱 에러) (((data-data.mean())**2)).mean() #RMSE(제곱->루트 에러) np.sqrt((((data-data.mean())**2)).mean())
 matplotlib.dist_table
matplotlib.dist_table
dist_table=np.array([[(((data[i]-data[j])**2).sum())**0.5 for j in range(150)]for i in range(150)]) array([[0. , 0.53851648, 0.50990195, ..., 4.45982062, 4.65080638, 4.14004831], [0.53851648, 0. , 0.3 , ..., 4.49888875, 4.71805044, 4.15331193], [0.50990195, 0.3 , 0. , ..., 4.66154481, 4.84871117, 4.29883705], ..., [4.45982062, 4.49888875, 4.66154481, ..., 0. , 0.6164414 , 0.64031242], [4.6508063..
(((data-data[0])**2).sum(axis=1))**0.5 array([0. , 0.53851648, 0.50990195, 0.64807407, 0.14142136, 0.6164414 , 0.51961524, 0.17320508, 0.92195445, 0.46904158, 0.37416574, 0.37416574, 0.59160798, 0.99498744, 0.88317609, 1.1045361 , 0.54772256, 0.1 , 0.74161985, 0.33166248, 0.43588989, 0.3 , 0.64807407, 0.46904158, 0.59160798, 0.54772256, 0.31622777, 0.14142136, 0.14142136, 0.53851648, 0.53851648,..
 sklearn.LinearRegression(선형회기)
sklearn.LinearRegression(선형회기)
회기 분석 세가지가 데이터를 넣어서 나머지 한 개의 데이터를 예측 X=data[:,:3] y=data[:,3] from sklearn.linear_model import LinearRegression model=LinearRegression() model.fit(X,y) model.score(X,y) 0.9380481344518986 pred_y=model.predict(X) y,pred_y 더보기 (array([0.2, 0.2, 0.2, 0.2, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.2, 0.2, 0.1, 0.1, 0.2, 0.4, 0.4, 0.3, 0.3, 0.3, 0.2, 0.4, 0.2, 0.5, 0.2, 0.2, 0.4, 0.2, 0.2, 0.2, 0.2, 0.4, 0.1, ..
