반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- Keras
- tensorflow
- CES 2O21 참가
- web
- mglearn
- web 용어
- 대이터
- paragraph
- 머신러닝
- vscode
- pycharm
- C언어
- html
- 재귀함수
- classification
- broscoding
- KNeighborsClassifier
- cudnn
- CES 2O21 참여
- postorder
- java역사
- web 개발
- 웹 용어
- web 사진
- bccard
- 데이터전문기관
- 자료구조
- inorder
- discrete_scatter
- 결합전문기관
Archives
- Today
- Total
bro's coding
neural_network.logisticRegression.원리알기 본문
반응형
data : breast cancer data[0,1]
cost : BCE(binary cross entropy)
import numpy as np
import matplotlib.pyplot as plt
# data 준비
from sklearn.datasets import load_breast_cancer
cancer=load_breast_cancer()
X=cancer.data[:,[0,1]]
# normalization
X_norm=(X-X.mean(axis=0))/X.std(axis=0)
y=cancer.target
# 초기화(random값을 사용해도 좋음)
w=np.array([1,1])
b=0
# check 변화량의 크기
c=0.1
# cost 기록
cost_log=[]
# 결과값을 확률로 바꿔주기 위한 sigmoid function
def sigmoid(t):
return 1/(1+np.exp(-t))
pred_y=sigmoid(X_norm@w+b)
# BCE(binary cross entropy)
cost=(-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean()
for i in range(1000):
new_w=w
new_b=b
t_cost=[]
# w[0] + - c 에 대한 cost
pred_y=sigmoid(X_norm@(w+[c,0])+b)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
pred_y=sigmoid(X_norm@(w-[c,0])+b)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
# w[1] + - c 에 대한 cost
pred_y=sigmoid(X_norm@(w+[0,c])+b)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
pred_y=sigmoid(X_norm@(w-[0,c])+b)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
# b + - c 에 대한 cost
pred_y=sigmoid(X_norm@w+b+c)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
pred_y=sigmoid(X_norm@w+b-c)
t_cost.append((-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean())
# 더이상 줄어들지 않으면 break
if cost<np.min(t_cost):
break
# w[0] 관련
# 기존 cost보다 작고,[w[0] + c]의 cost<[w[0] - c]의 cost
if t_cost[0]<=t_cost[1] and t_cost[0]<cost:
new_w=w+[c,0]
# 기존 cost보다 작고,[w[0] + c]의 cost>[w[0] - c]의 cost
elif t_cost[0]>t_cost[1] and t_cost[1]<cost:
new_w=w-[c,0]
# w[1] 관련
# 기존 cost보다 작고,[w[1] + c]의 cost<[w[1] - c]의 cost
if t_cost[2]<=t_cost[3] and t_cost[2]<cost:
new_w=w+[0,c]
# 기존 cost보다 작고,[w[1] + c]의 cost>[w[1] - c]의 cost
elif t_cost[2]>t_cost[3] and t_cost[3]<cost:
new_w=w-[0,c]
# b 관련
# 기존 cost보다 작고,[b + c]의 cost<[b - c]의 cost
if t_cost[4]<=t_cost[5] and t_cost[4]<cost:
new_b=b+c
# 기존 cost보다 작고,[b + c]의 cost>[b - c]의 cost
elif t_cost[4]>t_cost[5] and t_cost[5]<cost:
new_b=b-c
# 찾아낸 w, b 값을 assign
w=new_w
b=new_b
# cost 기록
pred_y=sigmoid(X_norm@w+b)
cost=(-(y*np.log(pred_y)+(1-y)*np.log(1-pred_y))).mean()
cost_log.append(cost)
print(i, w, b, cost)
# 80 [-3.7 -0.9] 0.7 0.25586907503308465
plt.plot(cost_log)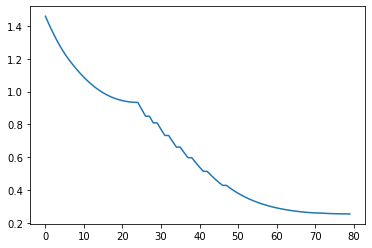
# LogisticRegression과 비교
from sklearn.linear_model import LogisticRegression
model=LogisticRegression()
model.fit(X_norm,y)
model.coef_[0],model.intercept_
# (array([-3.33675305, -0.87487424]), array([0.6851967]))반응형
'[AI] > python.Neural_Network' 카테고리의 다른 글
| 다중 분류 원리 (0) | 2020.05.08 |
|---|---|
| 경사하강법 (0) | 2020.05.08 |
| 중간층 만들기(분류) (0) | 2020.05.07 |
| 중간층 만들기(값예측) (0) | 2020.05.07 |
| activation function(활성 함수) (0) | 2020.05.07 |
Comments


